Python и нейронные сети

Python и нейронные сети Python 08.12.2010

Искусственные нейронные сети (ИНС) — математические модели, а также их программные или аппаратные реализации, построенные по принципу организации и функционирования биологических нейронных сетей — сетей нервных клеток живого организма.

ИНС представляют собой систему соединённых и взаимодействующих между собой простых процессоров (искусственных нейронов).

Нейронные сети не программируются в привычном смысле этого слова, они обучаются. Возможность обучения — одно из главных преимуществ нейронных сетей перед традиционными алгоритмами. wikipedia

Содержание

Основные свойства
Решаемые проблемы
Виды архитектур
Правила обучения
Функции активации
Модули python для нейронных сетей
Простой пример

Основные свойства

Нейронные сети были вдохновлены нашим собственным мозгом. Модель стандартного нейрона изобретена более пятидесяти лет назад и состоит из трех основных частей:

Дентрит(ы) (Dendrite) - ответственны за сбор поступающих сигналов;
Сома (Soma) - ответствена за основную обработку и суммирование сигналов;
Аксон (Axon) - отвечает за передачу сигналов другим дендритам.

Работу нейрона можно описать примерно так: дендриды собирают сигналы, полученные от других нейронов, затем сомы выполняют суммирование и вычисление сигналов и данных, и наконец на основе результата обработки могут "сказать" аксонам передать сигнал дальше. Передача далее зависит от ряда факторов, но мы можем смоделировать это поведение как передаточную функцию, которая принимает входные данные, обрабатывает их и готовит выходные данные, если выполняются свойства передаточной функции.

Биологический нейрон - сложная система, математическая модель которого до сих пор полностью не построена. Введено множество моделей, различающихся вычислительной сложностью и сходством с реальным нейроном. Одна из важнейших - формальный нейрон (ФН). Несмотря на простоту ФН, сети, построенные из таких нейронов, могут сформировать произвольную много мерную функцию на выходе (источник: Заенцев И. В. Нейронные сети: основные модели).

Нейрон состоит из взвешенного сумматора и нелинейного элемента. Функционирование нейрона определяется формулами:

где

x_i - входные сигналы, совокупность всех входных сигналов нейрона образует вектор x;
w_i - весовые коэффициенты, совокупность весовых коэффициентов образует вектор весов w;
NET - взвешенная сумма входных сигналов, значение NET передается на нелинейный элемент;
θ — пороговый уровень данного нейрона;
F — нелинейная функция, называемая функцией активации.

Нейрон имеет несколько входных сигналов x и один выходной сигнал OUT. Параметрами нейрона, определяющими его работу, являются: вектор весов w, пороговый уровень θ и вид функции активации F.

Нейронные сети привлекают к себе внимание за счет следующих возможностей:

способны решать трудно формализуемые задачи;
присущ параллельный принцип работы, что очень важно при обработке больших объемов данных;
способность к обучению и способность к обобщению;
толерантность к ошибкам;

К основным свойствам нейронных сетей можно отнести:

Способность обучаться. Нейронные сети не программируются, а обучаются на примерах. После предъявления входных сигналов (возможно, вместе с требуемыми выходами) сеть настраивают свои параметры таким образом, чтобы обеспечивать требуемую реакцию.
Обобщение. Отклик сети после обучения может быть до некоторой степени нечувствителен к небольшим изменениям входных сигналов. Эта внутренне присущая способность "видеть"" образ сквозь шум и искажения очень важна для распознавания образов. Важно отметить, что искусственная нейронная сеть делает обобщения автоматически благодаря своей структуре, а не с помощью использования "человеческого интеллекта"" в форме специально написанных компьютерных программ.
Параллелизм. Информация в сети обрабатывается параллельно, что позволяет достаточно выполнять сложную обработку данных с помощью большого числа простых устройств.
Высокая надежность. Сеть может правильно функционировать даже при выходе из строя части нейронов, за счет того, что вычисления производятся локально и параллельно.

Алгоритм решения задач с помощью многослойного персептрона (источник: Заенцев И. В. Нейронные сети: основные модели)

Чтобы построить многослойный персептрон, необходимо выбрать его параметры. Чаще всего выбор значений весов и порогов требует обучения, т.е. пошаговых изменений весовых коэффициентов и пороговых уровней.

Общий алгоритм решения:

Определить, какой смысл вкладывается в компоненты входного вектора x. Входной вектор должен содержать формализованное условие задачи, т.е. всю информацию, необходимую для получения ответа.
Выбрать выходной вектор y таким образом, чтобы его компоненты содержали полный ответ поставленной задачи.
Выбрать вид нелинейности в нейронах (функцию активации). При этом желательно учесть специфику задачи, т.к. удачный выбор сократит время обучения.
Выбрать число слоев и нейронов в слое.
Задать диапазон изменения входов, выходов, весов и пороговых уровней, учитывая множество значений выбранной функции активации.
Присвоить начальные значения весовым коэффициентам и пороговым уровням и дополнительным параметрам (например, крутизне функции активации, если она будет настраиваться при обучении). Начальные значения не должны быть большими, чтобы нейроны не оказались в насыщении (на горизонтальном участке функции активации), иначе обучение будет очень медленным. Начальные значения не должны быть и слишком малыми, чтобы выходы большей части нейронов не были равны нулю, иначе обучение также замедлится.
Провести обучение, т.е. подобрать параметры сети так, чтобы задача решалась наилучшим образом. По окончании обучения сеть готова решить задачи того типа, которым она обучена.
Подать на вход сети условия задачи в виде вектора x. Рассчитать выходной вектор y, который и даст формализованное решение задачи.

Решаемые проблемы

Проблемы решаемые с помощью нейронных сетей (источник).

Классификация образов. Задача состоит в указании принадлежности входного образа (например, речевого сигнала или рукописного символа), представленного вектором признаков, одному или нескольким предварительно определенным классам. К известным приложениям относятся распознавание букв, распознавание речи, классификация сигнала электрокардиограммы, классификация клеток крови.
Кластеризация/категоризация. При решении задачи кластеризации, которая известна также как классификация образов "без учителя", отсутствует обучающая выборка с метками классов. Алгоритм кластеризации основан на подобии образов и размещает близкие образы в один кластер. Известны случаи применения кластеризации для извлечения знаний, сжатия данных и исследования свойств данных.
Аппроксимация функций. Предположим, что имеется обучающая выборка ((x1,y1), (x2,y2)..., (xn,yn)) (пары данных вход-выход), которая генерируется неизвестной функцией (x), искаженной шумом. Задача аппроксимации состоит в нахождении оценки неизвестной функции (x). Аппроксимация функций необходима при решении многочисленных инженерных и научных задач моделирования.
Предсказание/прогноз. Пусть заданы n дискретных отсчетов {y(t1), y(t2)..., y(tn)} в последовательные моменты времени t1, t2,..., tn . Задача состоит в предсказании значения y(tn+1) в некоторый будущий момент времени tn+1. Предсказание/прогноз имеют значительное влияние на принятие решений в бизнесе, науке и технике. Предсказание цен на фондовой бирже и прогноз погоды являются типичными приложениями техники предсказания/прогноза.
Оптимизация. Многочисленные проблемы в математике, статистике, технике, науке, медицине и экономике могут рассматриваться как проблемы оптимизации. Задачей алгоритма оптимизации является нахождение такого решения, которое удовлетворяет системе ограничений и максимизирует или минимизирует целевую функцию. Задача коммивояжера, относящаяся к классу NP-полных, является классическим примером задачи оптимизации.
Память, адресуемая по содержанию. В модели вычислений фон Неймана обращение к памяти доступно только посредством адреса, который не зависит от содержания памяти. Более того, если допущена ошибка в вычислении адреса, то может быть найдена совершенно иная информация. Ассоциативная память, или память, адресуемая по содержанию, доступна по указанию заданного содержания. Содержимое памяти может быть вызвано даже по частичному входу или искаженному содержанию. Ассоциативная память чрезвычайно желательна при создании мультимедийных информационных баз данных.
Управление. Рассмотрим динамическую систему, заданную совокупностью {u(t), y(t)}, где u(t) является входным управляющим воздействием, а y(t) - выходом системы в момент времени t. В системах управления с эталонной моделью целью управления является расчет такого входного воздействия u(t), при котором система следует по желаемой траектории, диктуемой эталонной моделью. Примером является оптимальное управление двигателем.

Виды архитектур

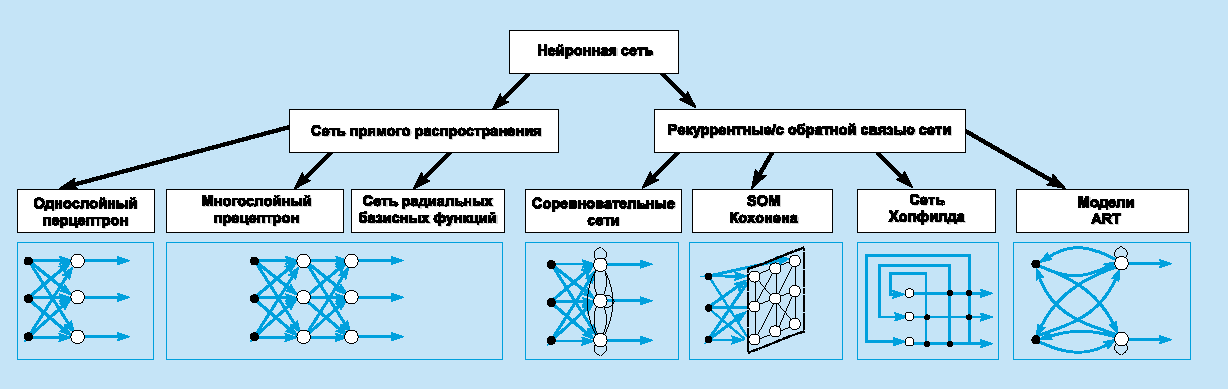
Архитектура нейронной сети - способ организации и связи отдельных элементов нейросети(нейронов). Архитектурные отличия самих нейронов заключаются главным образом в использовании различных активационных (возбуждающих) функций. По архитектуре связей нейронные сети можно разделить на два класса: сети прямого распространения и рекуррентные сети.

Классификация искусственных нейронных сетей по их архитектуре приведена на рисунке ниже.

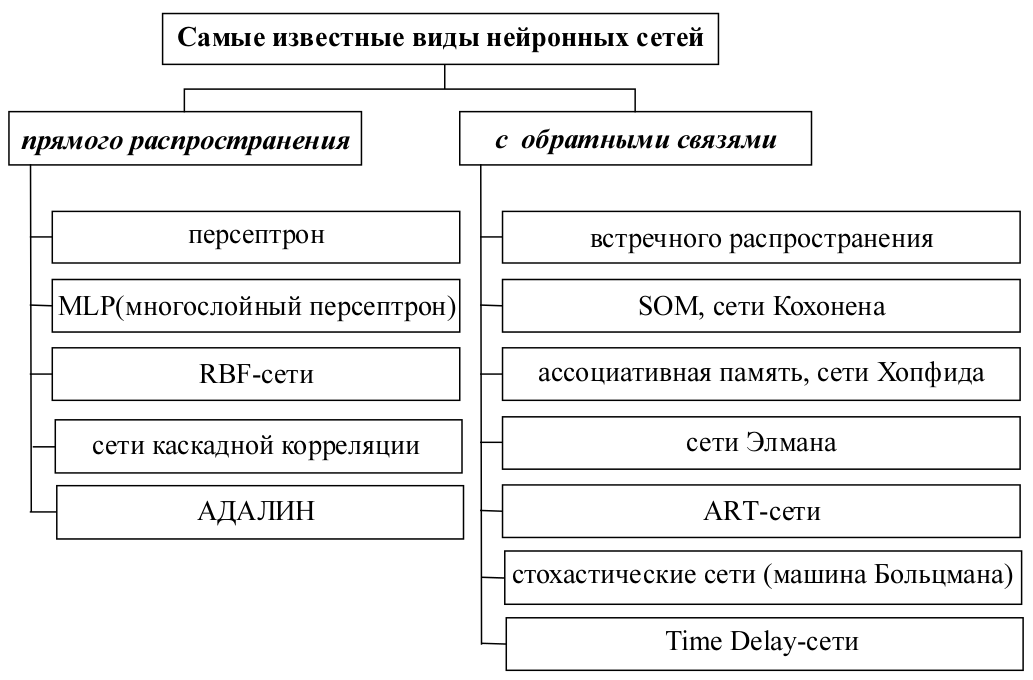
Похожая классификация, но немного расширенная

Сеть прямого распространения сигнала (сеть прямой передачи) - нейронная сеть без обратных связей (петель). В такой сети обработка информации носит однонаправленный характер: сигнал передается от слоя к слою в направлении от входного слоя нейросети к выходному. Выходной сигнал (ответ сети) гарантирован через заранее известное число шагов (равное числу слоев). Сети прямого распространения просты в реализации, хорошо изучены. Для решения сложных задач требуют большого числа нейронов.

Сравнительная таблица многослойного персепторна и RBF-сети

Многослойный персептрон	RBF-сети
Граница решения представляет собой пересечение гиперплоскостей	Граница решения - это пересечение гиперсфер, что задает границу более сложной формы
Сложная топология связей нейронов и слоев	Простая 2-слойная нейронная сеть
Сложный и медленно сходящийся алгоритм обучения	Быстрая процедура обучения: решение системы уравнений + кластеризация
Работа на небольшой обучающей выборке	Требуется значительное число обучающих данных для приемлемого результат
Универсальность применения: кластеризация, аппроксимация, управление и проч	Как правило, только аппроксимация функций и кластеризация

Рекуррентная сеть (сеть с обратными связями) - многослойная нейронная сеть, имеющая хотя бы один слой, выходные сигналы с которого поступают на этот же слой или на один из предыдущих слоев. В рекуррентной сети нейроны многократно участвуют в обработке каждой входной информации, что позволяет использовать некоторые динамические свойства нейросети. Использование обратных связей сокращает объем нейронной сети. На основе рекуррентных сетей разработаны различные модели ассоциативной памяти.

	Сети прямого распространения (без обратных связей)	Рекуррентные сети (с обратными связями)
Преимущества	Простота реализации. Гарантированная (математически доказанная) сходимость вычислений.	Меньший по сравнению с сетями прямого распространения объем сети(по количеству нейронов).
Недостатки	Быстрый рост числа нейронов с увеличением сложности задачи.	Необходимость использования дополнительных условий, обеспечивающих сходимость вычислений.

Искусственная нейронная сеть может рассматриваться как направленный граф со взвешенными связями, в котором искусственные нейроны являются узлами. По архитектуре связей искусственные нейронные сети могут быть сгруппированы в два класса: сети прямого распространения, в которых графы не имеют петель, и рекуррентные сети, или сети с обратными связями.

Сеть Хопфилда (адресуемая по содержанию ассоциативная память, модель Хопфилда) - нейронная сеть, состоящая из одного слоя нейронов, каждый из которых связан синапсами со всеми остальными нейронами, а также имеет один вход и один выход. Все нейроны используют жесткую пороговую функцию активации и могут давать на выходе два значения: -1 (заторможен) и +1 (возбужден). В модели используется принцип хранения информации как динамически устойчивых аттракторов. В процессе настройки сети уменьшается энергетическая функция, достигая локального минимума (аттрактора), в котором энергетическая функция сохраняет постоянное значение.

Сети Хопфилда отличаются следующими признаками

наличие обратных связей, идущих с выходов сетей на их входы по принципу "со всех на все";
расчет весовых коэффициентов нейронов проводится на основе исходной информации лишь перед началом функционирования сети, и все обучение сети сводится именно к этому расчету без обучающих итераций;
при предъявлении входного вектора, сеть "сходиться" к одному из запомненных в сети эталонов, представляющих множество равновесных точек, которые являются локальными минимумами функции энергии, содержащей в себе всю структуру взаимосвязей в сети;

Сеть Хемминга (Классификатор по минимуму расстояния Хемминга) - нейронная сеть ассоциативной памяти, принцип работы которой основан на вычислении расстояния Хемминга от входного вектора до всех векторов-образцов, известных сети. Сеть выбирает образец с наименьшим расстоянием Хемминга до входного вектора и выход, соответствующий этому образцу активизируется. Если сеть Хопфилда может восстанавливать зашумленные образы, то сеть Хемминга лишь указывает на соответствие входного образа одному из известных ей классов, а сам образ в ходе работы сети теряется.

В случае, если необходимо определить номер эталона, ближайший к предъявленному входному вектору, может быть использована сеть Хэмминга. Преимущество этой сети по сравнению с сетью Хопфилда являются меньшие затраты на память и объем вычислений.

Сеть Кохонена (SOM) состоит из одного слоя настраиваемых весов и функционирует в духе стратегии, согласно которой победитель забирает все, т.е. только один нейрон возбуждается, остальные выходы слоя подавляются. Сеть Кохонена осуществляет классификацию входных векторов в группы схожих, подстраивая веса таким образом, что входные образы, принадлежащие одному классу, будут активировать один и тот же выходной нейрон. Одно из важнейших свойств обучающей сети Кохонена - способность к обобщению. Вектор каждого из нейронов сети заменяет группу соответствующих ему классифицируемых векторов.

Виды нейронных сетей и их характеристики (по материалам книги В. В. Круглов, В. В. Борисов - Искусственные нейронные сети. Теория и практика)

Название нейронной сети	Область приминения	Недостатки	Преимущества
Искусственный резонанс - 1, ART-1 Network (Adaptive Resonance Theory Network - 1)	Распознавание образов, кластерный анализ	Неограниченное увеличение числа нейронов в процессе функционирования сети. При наличии шума возникает значительный проблемы, связанные с неконтролируемым ростом числа эталонов.	Обучение без учителя
Двунаправленная ассоциативная память (ДАП). Bi-Directional Associative Memory (BAM)	Ассоциативная память, распознавание образов.	Емкость ДАП жестко ограниченна, также ДАП обладает некоторой непредсказуемостью в процессе функционирования. Возможны ложные ответы.	По сравнению с автоассоциативной (например, с сетью Хопфилда), двунаправленная ассоциативная память дает возможность строить ассоциации между векторами X и Y, которые в общем случае имеют разные размерности. За счет таких возможностей гетероассоциативная память используется для более широкого класса приложений, чем автоассоциативная память. Процесс формирования синаптических весов является простым и достаточно быстрым. Сеть быстро сходиться в процессе функционирования.
Машина Больцмана (Boltzmann Machine)	Распознавание образов, классификация.	Медленный алгоритм обучения.	Алгоритм дает возможность сети выбираться из локальных минимумов адаптивного рельефа.
Обратное распространение (Neural Network with Back Propagation Training Algorithm)	Распознавание образов, классификация, прогнозирование, синтез речи, контроль, адаптивное управление, построение экспертных систем.	Многокритериальная задача оптимизации в методе обратного распространения рассматривается как набор однокритериальных - на каждой итерации происходит изменения значений параметров сети, улучшающих работу лишь с одним примером обучающей выборки. Такой подход существенно уменьшает скорость обучения. Классический метод обратного распространения относиться к алгоритмам с линейной сходимостью. Для увеличения скорости сходимости необходимо использовать матрицы вторых производных функций ошибки.	Обратное распространение - первый эффективный алгоритм обучения многослойных нейронных сетей. Один из самых популярных алгоритмом обучения, с его помощью решены и решаются многочисленных практические задачи.
Сесть встречного распространения (Counter Propagation Network)	Распознавание и восстановление образов (ассоциативная память), сжатие данных (с потерями), статистический анализ.	Сеть не дает возможность строить точные аппроксимации. В этом она значительно уступает сетям с обратным распространением ошибки. Слабая теоретическая проработка модификаций этой сети.	Сеть встречного распространения проста. Она дает возможность извлекать статистические характеристики из множества входных сигналов. Сеть быстро обучается. Время ее обучения по сравнению с обратным распространением может быть в 100 раз меньше. Сеть полезна для приложений, в которых требуется быстрая начальная аппроксимация. Сеть дает возможность строить функции и обратную к ней, что находит применения при решении практических задач.
Delta Bar Delta сеть	Распознавание образов, классификация.	Стандартный алгоритм DBD не использует эвристики, основанные на моменте. Даже небольшое линейное увеличение коэффициентов может привести к значительному росту скорости обучения, что вызовет скачки в пространстве весов. Геометрическое уменьшение коэффициентов иногда оказывается недостаточно быстрым.	Парадигма DBD является попыткой ускорить процесс конвергенции алгоритмов обратного распространения за счет использования дополнительное информации об изменении параметров и весов во время обучения.
Сеть поиска максимума с прямыми связями (Feed-Forward MAXNET)	Совместно с сетью Хэмминга, в составе нейросетевых систем распознавания образов.	Число слоев сети растет с увеличением размерности входного сигнала.	В отличие от сети MAXNET циклического функционирования, в рассматриваемой модели заранее известен объем вычислений, который требуется для получения решения.
Гауссов классификатор (Neural Gaussian Classifier)	Распознавание образов, классификация.	Примитивные разделяющие поверхности (гиперплоскости) дают возможность решать лишь самые простые задачи распознавания. Считаются априорно известными распределениями входных сигналов, соответствующих разным классам.	Программные или аппаратные реализации модели очень просты. Простой и быстрый алгоритм формирования синаптических весов и смещений.
Генетический алгоритм (Genetic Algorithm)	Распознавание образов, классификация, прогнозирование.	Сложные для понимания и программной реализации.	ГА особенно эффективны в поиске глобальных минимумов адаптивных рельефов, так как ими исследуются большие области допустимых значений параметров нейронных сетей. Достаточно высокая скорость обучения, хотя и меньшая, чем скорость сходимости градиентных алгоритмов. ГА дают возможность оперировать дискретным значениями параметров нейронных сетей, что упрощает аппаратную реализацию нейронных сетей и приводит к сокращению общего времени обучения.
Сеть Хэмминга (Hamming Net)	Распознавание образов, классификация, ассоциативная память, надежная передача сигналов в условиях помех	Сеть способна правильно распознавать (классифицировать) только слабо зашумленные входные сигналы. Возможность использования только бинарных входных сигналов существенно ограничивает область применения	Сеть работает предельно просто и быстро Выходной сигнал (решение задачи) формируется в результате прохода сигналов всего лишь через один слой нейронов Для сравнения: в многослойных сетях сигнал проходит через несколько слоев, в сетях циклического функционирования сигнал многократно проходит через нейроны сети, причем число итераций, необходимое для получения решения, бывает заранее не известно В модели использован один из самых простых алгоритмов формирования синаптических весов и смещений сети В отличие от сети Хопфилда, емкость сети Хэмминга не зависит от размерности входного сигнала, она в точности равна количеству нейронов. Сеть Хопфилда с входным сигналом размерностью 100 может запомнить 10 образцов, при этом у нее будет 10000 синапсов У сети Хэмминга с такой же емкостью будет всего лишь 1000 синапсов.
Сеть Хопфилда (Hopfield Network)	Ассоциативная память, адресуемая по содержанию; распознавание образов; задачи оптимизации (в том числе, комбинаторной оптимизации).	Сеть обладает небольшой емкостью. Кроме того, наряду с запомненными обрезами в сети хранятся и их 'негативы'. Размерность и тип входных сигналов совпадают с размерностью и типом выходных сигналов. Это существенно ограничивает применение сети в задачах распознавания образов. При использовании сильно коррелированных векторов-образцов возможно зацикливание сети в процессе функционирования. Квадратичные рост числе синапсов при увеличении размерности входного сигнала.	Позволяет восстановить искаженные сигналы.
Входная звезда (Instsr)	Может быть использована в сетях распознавания обрезов.	Каждая заезда а отдельности реализует слишком простую функцию. Из таких звезд невозможно построить нейронную сеть, которая реализовала бы любое заданное отображение Это ограничивает практическое применение входных звезд.	Входная заезда хорошо моделирует некоторые функции компонентов биологических нейронных сетей и может быть достаточна хорошей моделью отдельных участков мозга. При решении практических задач входные заезды могут быть использованы для построения простых быстро обучаемых сетей.
Сеть Кохонена (Kohonen's Neural Network)	Кластерный анализ, распознавание образов, классификации.	Сеть может быть использована для кластерного анализа только в случае, если заранее известно число кластеров.	В отличие от сети ART, сеть Кохонена способна функционировать в условиях помех, так как число классов фиксировано, веса модифицируются медленно, и настройка весов заканчивается после обучения (в сети АВТ настройка продолжается непрерывно)
Сеть поиска максимума (MAXNET)	Совместно с сетью Хэмминга, в составе нейросетевых систем распознавания образов.	Заранее не известно число итераций функционирования нейронной сети MAXNET. Она определяет, какой из входных сигналов имеет максимальное значение. Однако, в процессе функционирования сеть не сохраняет само значение максимального сигнала. Квадратичный рост числа синапсов при увеличении размерности входного сигнала.	Простата работы сети.
Выходная звезда (Outstsr)	Может быть использована как компонент нейронных сетей для распознавания образов.	Каждая звезда в отдельности реализует слишком простую функцию. Вычислительные возможности нейронных сетей, составленных из таких звезд, ограничены.	При решении практических задач выходные заезды могут быть использованы для построения простых быстро обучаемых сетей.
Сеть радиального основания (Radial Basis Function Network)	Распознавание образов, классификация.	Заранее должно быть известно числа эталонов, а также эвристики для построения активационных функций нейронов скрытого слоя. Сети этого типа довольно компактны и быстро обучаются. Радиально базисная сеть обладает следующими особенностями: один скрытый слой, только нейроны скрытого слоя имеют нелинейную активационную функцию и синаптические веса входного и скрытого слоев равны единицы.	Отсутствие этапа обучения в принятом смысле этого слова.
Нейронные сети, имитирующие отжиг (Neural Networks with Simulated Annealing Training Algorithm)	С помощью алгоритма имитации отжита можно строить отображения векторов различной размерности. K построению таких отображений сводятся многие задачи распознавания образов, адаптивного управления, многопараметрической идентификации, прогнозирования и диагностики.	Низкая скорость сходимости при обучении нейронных сетей большой размерности.	"Тепловые флуктуации", заложенные в алгоритм, дают возможность избегать локальных минимумов. Показано, что алгоритм имитации отжига может быть использован для поиска глобального оптимума адаптивного рельефа нейронной сети.
Однослойный персептрон (Single Layer Perceptron)	Распознавание образов, классификация.	Простые разделяющие поверхности (гиперплоскости) дают возможность решать лишь несложные задачи распознавания.	Программные или аппаратные реализации модели очень просты. Простой и быстрый алгоритм обучения.

Выбор количества нейронов и слоев (источник: Заенцев И. В. Нейронные сети: основные модели)

Нет строго определенной процедуры для выбора количества нейронов и количества слоев в сети. Чем больше количество нейронов и слоев, тем шире возможности сети, тем медленнее она обучает ся и работает и тем более нелинейной может быть зависимость вход выход.

Количество нейронов и слоев связано:

со сложностью задачи;
с количеством данных для обучения;
с требуемым количеством входов и выходов сети;
с имеющимися ресурсами: памятью и быстродействием машины, на которой моделируется сеть;

Были попытки записать эмпирические формулы для числа слоев и нейронов, но применимость формул оказалась очень ограниченной.

Если в сети слишком мало нейронов или слоев:

сеть не обучится и ошибка при работе сети останется большой;
на выходе сети не будут передаваться резкие колебания аппроксимируемой функции y(x).

Превышение требуемого количества нейронов тоже мешает работе сети.

Если нейронов или слоев слишком много:

быстродействие будет низким, а памяти потребуется много — на фон неймановских ЭВМ;
сеть переобучится: выходной вектор будет передавать незначительные и несущественные де тали в изучаемой зависимости y(x), например, шум или ошибочные данные;
зависимость выхода от входа окажется резко нелинейной: выходной вектор будет существен но и непредсказуемо меняться при малом изменении входного вектора x;
сеть будет неспособна к обобщению: в области, где нет или мало известных точек функции y(x) выходной вектор будет случаен и непредсказуем, не будет адекватен решамой задаче.

Правила обучения

Существуют три парадигмы обучения: с учителем, без учителя (самообучение) и смешанная. В первом случае нейронная сеть располагает правильными ответами (выходами сети) на каждый входной пример. Веса настраиваются так, чтобы сеть производила ответы как можно более близкие к известным правильным ответам. Усиленный вариант обучения с учителем предполагает, что известна только критическая оценка правильности выхода нейронной сети, но не сами правильные значения выхода. Обучение без учителя не требует знания правильных ответов на каждый пример обучающей выборки.

Известны 4 основных типа правил обучения:

коррекция по ошибке:
машина Больцмана;
правило Хебба;
обучение методом соревнования;

Известные алгоритмы обучения (по материалам книги В. В. Круглов, В. В. Борисов - Искусственные нейронные сети. Теория и практика)

Парадигма	Обучающие правило	Архитектура нейронной сети	Алгоритм обучения	Задачи
С учителем	Коррекция ошибок	Однослойный и многослойный персептрон	Алгоритмы обучения персептрона. Обратное распространение, Adaline и Madaline	Классификация образов. Аппроксимация функций. Предсказание. Управление.
	Больцман	Рекурентная	Алгоритм обучения Больцмана	Классификация образов.
	Хебб	Многослойная прямого распространения	Линейный дискриминантный анализ	Анализ данных. Классификация образов.
	Соревнование	Соревнование	Векторное квантование	Категоризация внутри класса, сжатие данных
		Сеть ART	ART Map	Классификация образов
Без учителя	Коррекция ошибки	Многослойная прямого распространения	Проекция Саммона	Категоризация внутри класса, сжатие данных. Анализ данных.
	Хебб	Прямого распространения или соревнование	Метод главных компонентов	Анализ данных. Сжатие данных
		Сеть Хопфилда	Обучение ассоциативной памяти	Ассоциативная память
	Соревнование	Соревнование	Векторное квантование	Категоризация. Сжатие данных.
		SOM Кохонена	SOM Кохонена	Категоризация. Анализ данных.
		Сеть ART	ART1, ART2	Категоризация
Смешанная	Коррекция ошибки и соревнование	Сеть RBFN	Алгоритм обучения RBFN	Классификация образов. Аппроксимация функций. Предсказание. Управление.

Сети, реализующие парадигму самообучения (без учителя), предназначены, как правило, для анализа внутренней латентной структуры входной информации и решают задачи автоматической классификации, кластеризации, факторного анализа, компрессии данных. Обучающий алгоритм подстраивает веса сети так чтобы предъявление достаточно близких входных векторов давало одинаковые выходы. Процесс обучения, следовательно, выделяет статистические свойства обучающего множества и группирует сходные векторы в классы.

Функции активации

Активационная функция (функция активации, функция возбуждения, характеристическая функция) - нелинейная функция, вычисляющая выходной сигнал формального нейрона (OUT). Обычно принимает в качестве аргумента сигнал, получаемый на выходе входного сумматора (NET). В качестве активационных часто используются функции:

Жесткая пороговая функция

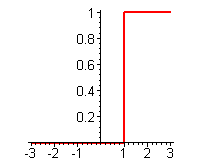
Используется в классическом формальном нейроне. Функция вычисляется двумя тремя машинными инструкциями, поэтому нейроны с такой нелинейностью требуют малых вычислительных затрат. Эта функция чрезмерно упрощена и не позволяет моделировать схемы с непрерывными сигналами. Отсутствие первой производной затрудняет применение градиентных методов для обучения та ких нейронов.

Линейный порог

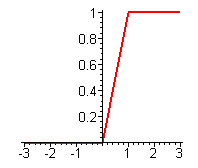
Линейный порог - кусочно-линейная функция, используемая в качестве активационной функции в формальном нейроне. Как видно из рисунка, есть два линейных участка, где функция тождественно равна минимально допустимому и максимально допустимому значению и есть участок, на котором функция строго монотонно возрастает.

Сигмоидальная функция

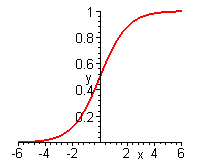
Сигмоидальная функция (сигмоидная функция, сигмоид, сигмоида) - монотонно возрастающая всюду дифференцируемая S-образная нелинейная функция с насыщением, которую очень удобно использовать в формальном нейроне в качестве функции активации. Сигмоид позволяет усиливать слабые сигналы и не насыщаться от сильных сигналов.

Среди однопараметрических наиболее распространены сигмоидальные функции следующих видов:

Логистическая функция
Гиперболический тангенс
Рациональная сигмоида

Применяется очень часто для многослойных перцептронов и других сетей с непрерывными сигналами. Гладкость, непрерывность функции - важные положительные качества. Непрерывность первой производной позволяет обучать сеть градиентными методами (например, метод обратного распространения ошибки, см. также недостатки алгоритма обратного распространения ошибки).

Значение производной легко выражается через саму функцию. Быстрый расчет производной ускоряет обучение.

Гауссова кривая

Применяется в случаях, когда реакция нейрона должна быть максимальной для некоторого определенного значения NET.

Градиентное обучение - общий способ оптимизации нейронной сети, в котором минимизация функционала ошибки осуществляется по методу градиентного спуска. Примером градиентного обучения многослойного персептрона служит семейство методов обратного распространения ошибки.

Функция ошибок (функционал ошибок, функция ошибки) - целевая функция, требующая минимизации в процессе управляемого обучения нейронной сети. Функция ошибок позволяет оценить качество работы нейронной сети во время обучения.

Подробнее с нейронными сетями можно познакомится по следующим ссылкам:

Модули python для нейронных сетей

Простой пример

В качестве примера приведу простую нейроную сеть (простой персептрон), которая после обучения сможет распознавать летающие объекты, не все, а только чайку :), все остальные входные образы будут распознаваться как НЛО.

# encoding=utf8
import random

class NN:
    def __init__(self, threshold, size):
        """
        Установим начальные параметры.
        """
        self.threshold = threshold
        self.size = size
        self.init_weight()

    def init_weight(self):
        """
        Инициализируем матрицу весов случайными данными.
        """

        self.weights = [[random.randint(1, 10) for i in xrange(self.size)] for j in xrange(self.size)]

    def check(self, sample):
        """
        Считаем выходной сигнал для образа sample. Если vsum > self.threshold то можно предположить, что в sample есть образ чайки.
        """

        vsum = 0
        for i in xrange(self.size):
            for j in xrange(self.size):
                vsum += self.weights[i][j] * sample[i][j]

        if vsum > self.threshold:
            return True
        else:
            return False

    def teach(self, sample):
        """
        Обучение нейронной сети.
        """

        for i in xrange(self.size):
            for j in xrange(self.size):
                self.weights[i][j] += sample[i][j]

nn = NN(20, 6)

# Обучаем нейронную сеть.

tsample1 = [
    [0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 1],
    [0, 0, 0, 0, 1, 0],
    [0, 1, 0, 1, 0, 0],
    [0, 0, 1, 0, 0, 0],
    [0, 0, 0, 0, 0, 0],
]
nn.teach(tsample1)

tsample2 = [
    [0, 0, 0, 0, 1, 0],
    [0, 0, 0, 1, 0, 0],
    [1, 0, 1, 0, 0, 0],
    [0, 1, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0],
]
nn.teach(tsample2)

tsample3 = [
    [0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 1, 0],
    [0, 0, 0, 1, 0, 0],
    [1, 0, 1, 0, 0, 0],
    [0, 1, 0, 0, 0, 0],
]
nn.teach(tsample3)

tsample4 = [
    [0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 1],
    [0, 0, 1, 0, 1, 0],
    [0, 0, 0, 1, 0, 0],
]
nn.teach(tsample4)

# Проверим что может нейронная сеть.

# Передадим образ чайки, который примерно похож на тот, про который знает персептрон. 
wsample1 = [
    [0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0],
    [0, 0, 0, 1, 0, 0],
    [1, 0, 1, 0, 0, 0],
    [0, 1, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0],
]

print u"чайка" if nn.check(wsample1) else u"НЛО"

# Передадим неизвестный образ. 
wsample2 = [
    [0, 0, 0, 0, 0, 0],
    [0, 0, 1, 0, 0, 0],
    [0, 0, 0, 1, 0, 0],
    [0, 0, 1, 0, 0, 0],
    [0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0],
]

print u"чайка" if nn.check(wsample2) else u"НЛО"

# Передадим образ чайки, который примерно похож на тот, про который знает персептрон. 
wsample3 = [
    [0, 0, 0, 0, 1, 0],
    [0, 1, 0, 1, 0, 0],
    [0, 0, 1, 0, 0, 0],
    [0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0],
]

print u"чайка" if nn.check(wsample3) else u"НЛО"

Результаты

# первый запуск 
чайка       # True
НЛО         # True
чайка       # True

# второй запуск 
НЛО         # False
НЛО         # True
чайка       # True

У приведенной реализации есть несколько слабостей, для данного примера вполне терпимых :) :

малая обучаемая выборка, потому персептрон иногда может ошибаться
веса выбираются случайно, каждый раз при запуске, в идеале их нужно было бы сохранять после обучения
отсутствует обратный проход, после которого сеть корректирует свои веса и лучше адаптируется к новым данным

PS: Подсветка кода немного лагает, потому сорцы лучше смотреть в любимом текстовом редакторе.

Дополнительное чтиво

Python и нейронные сети Python 08.12.2010

Цитата

Категории

Архив ↓